In these hi-tech electronic times we can take for granted our ready access to calculating aids, whether it is a free app on our smartphones, laptop or the powerful pocket calculators which are now so cheap that it's hardly worth replacing the batteries (assuming it's not solar powered). The history of the development of calculating aids from the earliest times to the present day is a fascinating one and there are a wide variety of resources both online and in print.

My brother Ian's and my main interest are in slide rules both as collectables and in use but it has extended in a modest way to the wider history of portable calculating aids. Below is an image gallery of examples of some typical designs of aids we possess which in their earliest forms span over twenty centuries. Comments are included on some points of interest with links to in-depth resources describing their history and use. The selection by no means covers all aspects of the history, there are huge gaps e.g. the many designs of mechanical calculators which due to their bulk and/or cost do not form part of our tiny collection.

Calculating aids appeal for not dissimilar reasons as to why microscopes and microscopy appeals. The aids and their design are of interest on many levels. Genuine antiques or recent collectables can be admired for their design and build, their key role in the history of calculating as well as been usable. They also stretch our rather rusty school level mathematical skills exploring how they were used and also open many aspects on reading about their history and key characters involved in their development where appropriate.

Abacus - earliest forms known over 2000 years ago
The use of counting beads and later abaci in some form as a calculating aid has a very long history. The Wikipedia entry (link below) gives a good synopsis of the history (noting that the earliest known were Mesopotamian and Egyptian) and etymology of the term 'abacus'. The two modern examples illustrated below are available for a few pounds from many sources (these examples were from eBay UK). The lefthand model is a typical Chinese design or suanpan, the righthand model is a typical Japanese model or soroban. The latter has a resetting button for all the beads.

The basic principles are not difficult to acquire, with the lower single value beads and the upper five value beads being moved towards the beam when making a number entry. It is the mastery that is difficult (I haven't ventured much beyond basic principles), but the proficient can compete with an electronic calculator (see Wikipedia entry). Abacus use is still taught in schools in Japan. Only the thumb and forefinger are used for bead manipulation and addition, subtraction, multiplication and division is possible. There's a wide variety of free guides to download and a variety of designs to purchase. The number of rods in an abacus determine the largest numbers that can be manipulated.

The calculator maker Sharp introduced a model with an abacus built in, shown in the Wikipedia entry.



- 'The Abacus: one of the oldest Calculation Devices', Jörn Lütjens, Proceedings of the 9th International Meeting of Slide Rule Collectors, September, 2003 p118.
- 'Soroban, the Japanese Sophisticated Calculating Device', Werner H. Rudowski, UK Slide Rule Gazette. Issue 11 Autumn 2010, p43.
- Wikipedia entry Abacus, Suanpan and Soroban.
- 'An Abacus Abstract', Len Peach, UK Slide Rule Gazette. Issue 3 Autumn 2002. p75.
- Soroban. Useful Arithmetical Tool. Free manual in pdf format published by the League for Soroban Education of Japan, Inc.

Proportional compass - late 16thC
The proportional compass was developed in the later part of the 16thC and can still be bought new today. A finely crafted 2nd half of 19thC example is shown below signed 'J.&W.E. Archbutt.' '201 Westminster Bdg. Rd. London'. It is a typical 6.25 inches in length but longer examples were made. The principle is very simple but enables a limited set of calculation types to be made. It is a pair of dividers where the hinge is movable by the knurled knob; some examples have a rack and pinion to set the hinge more precisely. The typical full set of scales are inscribed i.e. 'Plans' and 'Solids' on one side and 'Circles' and 'Lines' on the other.

By setting a value on the Line scale inscribed from 1-8, this linear proportion is set between the pointers on both ends allowing e.g. measurements to be transferred from one technical drawing to another at different scale. The 'Plans' and 'Solids' scales allow the proportional scaling of two and three dimensional subjects by area and volume. 'Circles' was a neat feature (on this example inscribed from 6-20) that allowed polygons to be drawn in a given sized circle. e.g. if set '6' on 'Circles' scale and the larger points spacing are set to the radius of circle wish to draw, the smaller points allow an exact hexagon to be inscribed within it. Tomash and Williams in the reference below note that this scale could be useful e.g. for wheelwrights evenly setting spokes or for engineers setting gear cog spacings.





The line on pivot stock is aligned against a value on the chosen scale (e.g. '2' on 'Plans' scale as shown above) when the dividers are closed to ensure points keep alignment. After tightening knob, the clutch allows the divider point distances to be set.



Its size and typical lack of sub-divisions between the scale numbering limited its versatility and accuracy compared with the sector below. Some modern examples still have the full complement of original scales, others have restricted scales or none at all; the latter where it is now mainly used just for proportional linear scaling e.g. as a drawing aid.

- The Sector: its history, scales, and uses by Erwin Tomash and Michael R Williams. IEEE Annals of the History of Computing, 2003, vol. 25 (1), pp.34-37.
(Discusses the proportional compass as a precursor to the sector.)

Sector - late 1500s+ (also called a proportional compass)
The sector was a versatile calculating aid capable of a variety of computations of value to e.g. a navigator, surveyor or engineer. The sector is thought to have been invented by a number of people independently; English mathematician Thomas Hood and Galileo are two that are given credit for it. The sector uses the same principle of proportional triangles as the proportional compass above. The example below is an unnamed 19th century example and is the typical length of 6 inch folded and one foot unfolded. Often made of ivory or bone (some early forms were brass) it had a brass hinge to fold out or set at any desired angle.

Pairs of scales inscribed on each face are used in conjunction with a pair of normal dividers and the sector hinge angle to calculate a variety of functions using the principle of proportionality of similar triangles.





In addition to the paired scales, a triplet of scales that are very straightforward but satisfying to use are the three marked T, S and N formed when the sector is fully folded out. T and S are logarithmic degree scales to read their tangents and sines respectively directly off the log L scale. For example in the topmost image '30°' on the S scale aligns exactly with '5' on the L scales. i.e. sin 30° = 0.5. The log L scale is an example of a Gunter scale (see below) and is the simplest implementation of the use of a log scale for multiplication and division. The simplicity and versatility of logs can really be appreciated using this one scale, more so than a slide rule. It is designed to be used with compass / dividers as in the example shown above illustrating 3 x 2 = 6. The divider points are set using the scale to the first number, '3' in this case. Moving the divider to '2' then reads out '6' on the other point.



The three pairs of scales on this face are marked 'L, C, s and POL' with 'S, T and T' on reverse. A 12 inch rule runs along one edge. 'L' was the 'Line of Lines' a main scale used for multiplication and divsion. POL had a similar role to the 'Circles' scale on the proportional compass above. The other lines allowed various geometrical calculations.



To explore how sectors are used I have been reluctant to use dividers on antique examples. Otto van Poelje in a fascinating article discusses the potential damage of dividers with different needle styles on rules in article linked below. Wikipedia have a superb hi-res undistorted scan of a Dollond sector. Printing this out on stiff photo paper and using a DVD case* as a hinge allows a user to explore how sectors are used. (*The ingenious use of a CD/DVD case as a pivot for circular rules was described by Ying Hum on the International Slide Rule Museum website page on home made slide rules.)

One special form of sector was the 'Gunner's Compass' (or Sector / Calliper) which had curved inner edges and a hinge that allowed arms to be crossed. This was used for measuring cannon ball diameter, inner bore of cannons and various calculations required in artillery.

- 'The Sector: its history, scales, and uses' by Erwin Tomash and Michael R Williams. IEEE Annals of the History of Computing, 2003, vol. 25 (1), pp.34-37.
- Wikipedia entry Sector (Instrument)
- 'Which Dividers to use on Gunter rules', Otto E. van Poelje, Slide Rule Gazette. Issue 9 Autumn 2008, p65.

Napier's bones - 1617+
Shown right is a modern variant of Napier's bones (or rods) and is a form of abacus; this example from www.grand-illusions.co.uk. John Napier described his version in 1617 which Wikipedia notes is based on earlier calculating methods. They were an elegantly simple but powerful aid to complex multiplication and division. Some variants, not the one shown, can also do square roots. Napier's bones were square rods with numbered grids on all sides, the attractive example shown in engraved wood limits computation to a single use of each number unless duplicates of the strips are made. The sets can be easily made either in original form or as printed strips, many websites offer templates and instructions on their use. 

Even the set shown assembled for storage allows calculations to be read off which many would struggle to do in our head or take a little time with pen and paper. For example the white line shows 12345 x 7 (numbers on top and side edges). Just reading from right to left along white line, adding diagonals (including any 1's carried from the right where necessary), a user can read off the digits in the answer from right to left, i.e. 86415. In normal use, the 'rods' would be added or removed for the calculation of interest.

Wikipedia entry Napier's bones.

 

 

Logarithm tables - 1614+
In 1614 the Scotsman John Napier published his treatise on logarithms together with extensive tables of logs related to the present natural logs. The English mathematician Henry Briggs in liaison with Napier constructed tables of logs to the base ten which became the base most widely used. The potential of logarithms to transform complex multiplication and division to much simpler and less error prone operations using addition and subtraction was immediately recognised and proved invaluable, both in tabular form and their application in the form of slide rules.



The book above is a 1726 copy of Henry 'Sherwin's Tables' which compiled tables produced in the previous century by Henry Briggs, Dr. Wallis, Edmund Halley and Aubrey Sharp—all Savilian Professors of Geometry at the University of Oxford.

My brother and I keep an eye out for the tattiest examples of older books of interest (on microscopy and other topics) because they attract far less value than excellent examples (the book dealer had already priced it way below the value of good condition copies but immediately accepted our offer of half its marked price as suspect he thought he could finally be rid of it). But the extensively used and in this case heavily annotated editions are to us far more interesting. Every spare page of this example has copious notes by past users, their names and gives a book real character.



The calculation of the logs and associated trigonometric tables involved extensive manual work using various algorithms and its amazing to see the precision to which they are given. The early chapters describe thoroughly the calculating methods used. The page above shows the logs of all whole numbers from 1 - 100 and all primes between 100 - 200 to sixty decimal places! The book also contains a chapter by Edmund Halley on the 'The Quadrature of the Circle' i.e. methods of calculating pi and includes values up to 125 decimal places.



The bulk of the book is tables of logs to seven decimal places of the numbers from 1 - 100 000 followed by trig tables and their logs. Spare a thought for the patient typesetter of these type of books! Despite best efforts, some calculation and/or typographic errors in this sort of book were inevitable and prompted Charles Babbage in the 19th century to design his mechanical computers ('engines') that automated the calculating and printing process of table production.



With our interest in slide rules we were delighted to find one annotated page (left above) devoted to how to use an early slide rule, from the text it describes a special rule used in brewing for calculating the tax due. On the right is the typical four figure log tables students like myself at school in the 60s and early 70s would be all too familiar with; this example is my original well-thumbed copy of the time.

- 'The First Tables of Logarithms' - A Brief Chronology, Thomas Wyman, Journal of the Oughtred Society Vol. 18, No. 2, 2009. p33.
- Wikipedia entry 'John Napier'
- 'Sherwin's Tables' various free editions on www.archive.org. Note that the tables are back in print as facsimiles from various publishers. The example I have inspected published by 'Forgotten Books' is a disappointing transfer to print of one of the public domain copies with many unreadable or poorly readable pages.

Slide rule - 1620+
The slide rule was a practical application of Napier's description of logarithms. In 1620 the English mathematician Edmund Gunter made a logarithmic scale on a single rule, the Gunter rule or scale, and used a compass / dividers to perform calculations (see the Sector earlier). William Oughtred in 1622 is generally credited with using the sliding action of two Gunter rules to form the slide rule and avoiding the need for compasses. The sliding cursor with hairline was invented later. The typical 10 inch (25 cm) rule can at best give 3 - 4 significant figs but as has been widely commented, this was more than sufficient to build much of the engineering and technological marvels and satisfy the requirements of many scientific disciplines well into the 20th century.

My interest in slide rules was described and illustrated in a Dec. 2012 Micscape Lite article 'The Appeal of Slide Rules - For Use and as Collectables' but a selection of models acquired since writing it are presented below as slide rules in their many forms have a key role in the history of calculating aids. The opportunities to study them are wide ranging. The upper 10 inch model shown with case is the earliest possessed, a Faber 367 (German) ca. with a 'decimal keeping cursor', designed to help keep track of the decimal point in extended calculations. It has beautifully crafted celluloid engraved scales on boxwood.
The next is a Reiss Darmstadt (German) made of solid aluminium. Makers like Pickett (USA) also made metal rules but unlike Pickett the Reiss model is unpainted and has a brushed finish. The metal slide rules have a lovely solidity and weight to them. The reverse has trig functions.



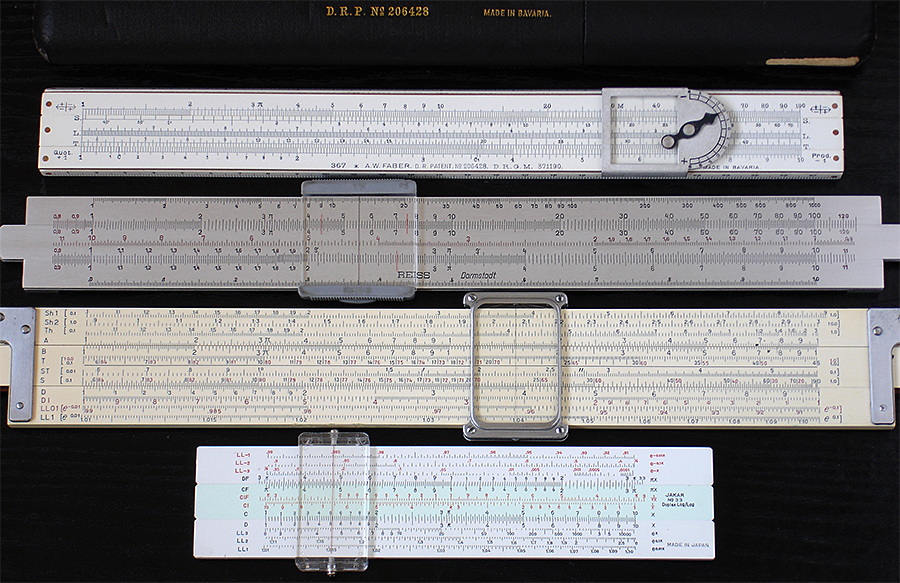
The third shown is a so-called vector rule because it has the hyperbolic functions sinh and tanh (Sh1 and 2, Th scales along top). This model is an American Dietzgen 1725 'Maniphase Multiplex Vector Trig Type Log Log Rule' (!). Such functions were important in fields such as electrical engineering. Vector rules are a relatively small sub-set of slide rules and have a particular interest amongst some collectors.

The fourth rule shown, although a diminutive 5 inch rule, the Japanese Jakar model 33 is a powerful 'pocket rocket' with scales both sides (duplex) offering a wide variety of functions. Unless a rarity or sought after classic, many rules fetch only a few pounds or modest double figure sums, mint in box examples attract more. The real rarities such as the Faber-Castell Mathema, one of the most powerful and complex mathematical models, can attract prices of £500 or more. One of the leading slide rule makers Faber-Castell (Germany) introduced an electronic calculator in 1972 (the TR series) with a slide rule on the back, which are now one of the most sought after collectables.

Some specialist slide rules are still made e.g. there are a wide range of circular rules available for the aviator.

The Oughtred Society Slide Rule Reference Manual, 2010 second edition, 102pp. Sumptuously illustrated in colour, available as a high quality softback from the Society, but they also generously offer a version as a free Acrobat file format download from their website as 'All About Slide Rules'.
'Slide Rules. A Journey Through Three Centuries', Dieter von Jezierski, Astragal Press, 2000, 126pp. A superb book.

Mechanical Calculating Devices - 1620s+
Historically, a progression of portable calculating aids would include the many variants of mechanical calculators developed in the 17th to 20th century. From the first mechanical calculators by Wilhelm Schickard, Blaise Pascal and Gottfried Wilhelm von Leibniz in the 17th century through to the many commercial 19th and 20th mechanical calculators found in offices and industry. A superb illustrated book surveying these as well as slide rules, electronic calculators and desktop computers is 'Antique Office Machines: 600 Years of Calculating Devices' by Thomas A. Russo. Schiffer Publishing 2001.

The only example we have is shown right—a small addiator (a Piccolo-S) for addition and subtraction. The leaflet code suggests it is dated 1974 but Wikipedia notes that the design dates back to 1889 and are often generically called addiators after a German maker Addiator Gesellschaft. A supplied metal stylus enables the operations to be performed on notched plates sandwiched between the outer plates and has a 'carry' facility. The pull-out bar at top clears all entries. There were many variants of these style of devices.

The German slide rule maker Faber-Castell had a range of pocket and full sized slide rules with an addiator on the back of the rule to complement the functions offered on the rule.

The many variants of mechanical calculator e.g. by famous names such as Burroughs and Remington were much more sophisticated than a simple addiator—many allowing arithmetical operations on multi-column numbers and were important tools in fields such as finance, commerce and certain science / engineering disciplines right up until the wide availability of computer facilities.

Wikipedia entry 'Addiator'.

Electronic pocket scientific calculator - 1972+
The crash of the slide rule industry must have been one of the fastest for a well established commercial product. The rapid development in both portable and increasingly affordable scientific calculators in the 1970s was responsible. A model widely cited as being key in the demise of the slide rule was the Hewlett Packard HP-35 shown left below with its original hard case and in detail below top right. It has all the functions the typical sophisticated slide rule could offer with more sig. figs. and no need to keep track of the exponent as is required with all slide rule calculations. This model was initially expensive when released in 1972 for $395 but widely embraced by many scientists and engineers. Prices plummeted for later models by HP and others. By 1975 sophisticated scientific calculators could be had in the UK for ca. £30 and I bought my first calculator (a Decimo 2001e 'Electronic slide rule') as a college student in 1975. My trusty Hemmi P280 was quickly banished to a cupboard but kept until a dormant interest in them was rekindled.



The resources on the 'Museum of HP Calculators' website (link below) discuss fascinating aspects of the development of the HP-35 and later models e.g. the tough design brief (squeezing HP's large desktop scientific calculator, the HP-9100, into a shirt pocket), developing keys that didn't have the 'oil can feel' of competitors and the algorithms used to give the desired results with the limited types of chips available. Many examples of the HP-35 were likely used to destruction but excellent examples can be found at modest cost as the example above.



Above left is the TI-55 issued in 1977. By this time calculators with sophisticated features including hyperbolics, statistics and programming were widely available and much more affordable. This near mint working example was £2-50 on eBay UK; away from the collectors' classics the many other past models often attract little interest. It is my day to day calculator as I like the classic lines and its operation compared to the more clinical complex modern models. It has 10 memories and useful functions not often seen nowadays - Δ% of two numbers and quick metric / imperial conversions.

Above right is one of the typical current sophisticated calculators including graphing facilities, the HP 39gII. Flagship graphing calculators like the Texas TI-NSpire range and Casio fx-CG20 have colour screens and many features to aid the learning of maths (e.g. studying the graph of shapes like curves and spirals using real images of shell cross sections, bridge arches etc.), although arguably these models become less cost effective when portable computers and smartphones can offer the same and more sophisticated features at higher screen resolution.

Calculators in their many hardware and software forms has tended to make their users lazy, I'm no exception, we may enter calculations we can do in our head and they give results to a ridiculous number of decimal places for most applications. In contrast the slide rule makes the user think of the calculations they are doing both to keep track of the exponent and estimate an approximate answer to ensure the calculation is entered and result read off correctly.

- Museum of HP Calculators. Classic Series Technology.
- The Demise of the Slide Rule (and the Advent of its Successors) by Otto van Poelje. Journal of the Oughtred Society Vol. 12, No. 2, Fall, 2003, p49
- Wikipedia HP-35 entry

Software based calculators - 20th-21stC+
With mobile devices like smartphones and portable computers being within easy reach for many users now, software based calculators will likely form an increasing role in our calculating requirements. Software based calculators allows more facilities to be offered with screens for general, scientific, statistical mode just a finger swipe or keypad stroke away. Customisation is also possible with some designs.



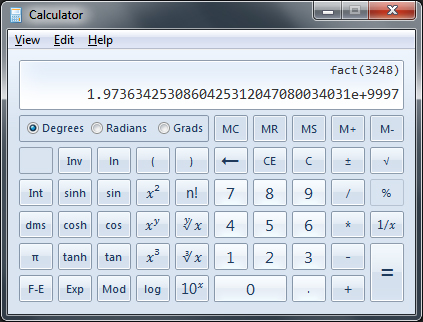
Shown left above is a typical free calculator app 'CalcMadeEasy' by Lalit Patil running on the iPod Touch with its touch sensitive screen. 69! is shown where the app retains the sensible limit of two figure exponents. On the right is the calculator offered as part of the Windows 7 operating system. The good folk at Microsoft have decided that four figure exponents need to be handled (allowing 3248! shown to be instantly calculated), despite the fact that it has been estimated e.g. by Roger Penrose in his book 'The Emperor's New Mind' that the number of baryons in the observable universe is of the order of 10⁸⁰. The help file notes that in scientific mode the results are precise to 32 sig. figs.

In a rather ironic twist there is now a wide selection of virtual slide rule apps offered for the iPod and iPad, some are beautifully crafted and based on real models from the past with super smooth friction free slider and cursors operated by deft finger swipes! Apps that mimic some of the classic calculators are also available.

What's next in calculating aid design? Who knows? It's a brave soul who makes predictions when today's electronics would have almost have seemed like magic barely a few decades earlier. Perhaps some development of Google's fledgling glasses where eye movements interact with a virtual calculator, or paper thin electronic displays that wrap around our wrist or form part of our clothing. Or maybe I'm being too narrow minded, perhaps some electronics that connects to and complements our brain functions, we may just think of the maths query and the result is input straight back to our brain.

Comments to the author David Walker are welcomed.

Footnote: Microscopy related calculating aids? To pacify fellow microscopy enthusiasts wondering why this article is in a microscopy magazine albeit under the banner 'Micscape Lite', I did endeavour to seek out calculating aids old or new used in microscopy. The only modern examples I have sourced to date are the two below although neither are strictly calculators or slide rules. I'd be interested to hear from readers who know of any others.

The first shown right is branded on the reverse 'Ted Pella, Inc. © 2008'. It presents look-up tables to allow a user to determine the actual size of a structure on a printed photomicrograph from a stated magnification, the result states what 1 mm on the print corresponds to in µm, nm or Å. Although commonly, there is a scale bar on the print or a statement on the scaling in a photomicrograph caption which avoids the need for this aid. With magnifications of 1 000 - 50 000 on one side and 50 000 - 100 000 on the reverse, it is primarily for electron microscopy. Although photomicrographs using optical microscopy at its highest optical mags of 1000 - 2 000 would just fit in the lowest range depending on print scale. The instructions note that higher mags than 100 000 can be calculated by dividing windowed values by 10.

The second shown right is made in the USA by Electron Microscopy Services and is single sided. This has the reverse function of the aid above i.e. it allows the microscopist to draw a scale bar of desired size in mm / cm on a printed photomicrograph when the subject's printed magnification is known. This aid has scales which can be used for magnifications spanning 100 - 3000X so can be used for both optical and electron microscopy. The scale bar is drawn in the arrowed notch bottom left when the known magnification on print has been set on the appropriate scale. The instructions note that a correction for a pen width of 0.25 mm has been made when drawing a scale. Manual corrections are necessary for thicker pens. Modern microscopes with dedicated camera / software systems have made this sort of aid increasingly unnecessary—calibration and embedding the desired scales into the digital photomicrograph (prior to printing) are built into the image capture / post-processing software.

Acknowledgements
Thank you to my brother Ian for loan of some of the items.
Thank you to William K Robinson, USA for the generous donation of the Dietzgen slide rule.
A number of the free access links above to specialist literature are hosted on Rod Lovett's website where he meticulously maintains a large database of specialist literature in collaboration with the appropriate journal / magazine publishers. He also presents his own resources on slide rules and a search engine to check past auction prices of different makes and models on eBay.

Microscopy UK Front Page
Micscape Magazine
Article Library

Please report any Web problems or offer general comments to the Micscape Editor .