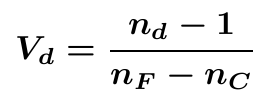
Dispersion staining is a technique that is commonly used to identify asbestos and many other materials. Although the term "Dispersion Staining" seems to imply adding dyes to materials, the coloured images that result from this technique are purely the result of an optical phenomenon.

The index of refraction (n) of a material is defined as the ratio of the velocity of light in vacuum (c) to the velocity of light in the material (v).

This can be expressed as a formula: n = c/v

When light passes from one material to another the light is refracted according to Snell's law:

n_a sin φ_a = n_b sin φ_b

n_a and n_b are the respective indices of refraction of the two materials, and φ_a and φ_b are the angles that the ray of light makes with a perpendicular to the plane of intersection of the two respective materials.

When n_a and n_b are equal the two angles φ_a and φ_b must be equal. Thus the path of light is not diverted when passing between two materials of equal refractive index.

The index of refraction at a given wavelength is constant in all directions for liquids and cubic solids. For uniaxial crystals (tetragonal and hexagonal) there are TWO indices of refraction at a given wavelength, and for biaxial crystals (orthorhombic, monoclinic, or triclinic) there are THREE indices of refraction at a given wavelength.

The index (or indices) of refraction of materials increases with decreasing wavelength. However, the rate of change of index of refraction with respect to changing wavelength is often highly variable from one substance to another. The change of index of refraction with wavelength is referred to as "dispersion". Dispersion is responsible for chromatic aberration in lenses.

The so-called "Abbe numbers" are used as a measure of a material's dispersion. Several different ones can be defined using different wavelength standards.

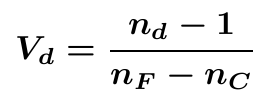
For the Abbe number, V_d, defined above, n_d is 587.6nm, n_F is 486.1nm, and n_C is 656.3nm.

Another common Abbe number is V_D. This one is similar to V_d except n_d is replaced with n_D, the value of this wavelength is 589.2nm.

Suppose one were to drop a glass rod into a liquid and illuminate the scene with monochromatic light. (Unstrained glass has the optical properties of a liquid, so it has only a single index of refraction.) If this glass rod have the identical index of refraction as the liquid, the rod will disappear as it is lowered into the liquid. If the glass rod has a different index of refraction, it will be visible because Snell's law will cause the light to bend as it passes between the liquid and glass phases.

Consider now what happens if one were to place a glass rod into a liquid and illuminate the scene with white light. (i.e. light with all wavelengths present across the visible spectrum.) If the dispersion of the glass and the liquid be even slightly different, it will be impossible to have the indices of refraction of the glass and the liquid be identical at all wavelengths. Suppose the indices of refraction of the glass and the liquid are equal at 650nm. Red light will pass from the glass to liquid without deviation, regardless of angle of incidence. But because of dispersion, the indices will NOT match at the short end of the spectrum, for example 450nm. Light of this wavelength will be refracted according the Snell's law by the differences in indices. The glass can be seen in the blue end of the spectrum, but not in the red—it thus appears to be coloured! This is dispersion staining!

Observation of dispersion staining in birefringent materials requires the use of polarising filters and rotating stages so that the materials can be oriented relative to polarised light so that only one of the indices of refraction of the material being studied is involved at a time. Thus when this technique is used in microscopy, it requires polarising microscopes.

Dispersion staining microscopy also requires the use of a special type of dark field illumination, and requires special dispersion staining objectives (DSO). Ordinary dark field illumination is achieved by having light illuminate the field of view with a hollow cone of light, with the inner numerical aperture of the cone being greater than the numerical aperture of the objective. Dispersion staining objectives are very different. They instead require a condenser with a VERY small numerical aperture, and place a centrable field stop in the objective so that all the light that goes straight through the objective is absorbed by this field stop. The light that is refracted passes around the field stop becomes visible.

The images of the dispersion staining objective near this text show such an objective from various view points.

The image to the left of this text shows an "end" view. Note the centrable field stop and the centring screws.

By carefully adjusting the condenser and field stop it is possible to detect only slight refraction from objects in the field of view, and thus only slight dispersion relative to the solvent.

The image below is taken utilising such a special dispersion staining objective with the central occulting disk. This image shows glass fibres embedded in an oil having an index of refraction that matches that of the fibres at the red end of the spectrum, but because of dispersion differences, not at the blue. The fibres are thus invisible in red but visible in blue, thus they appear to be blue in the image.

Because glass is not birefringent this effect can be observed without polarised light illumination.

The fibres are much less visible with this specimen when this is observed with ordinary dark field illumination instead of the special objective and they do not show the striking blue colour.

An interesting article on using dispersion staining to identify asbestos fibres can be found by clicking here. There is a link on their page to download a pdf version of the article. There are also colour images of images of asbestos fibres obtained with dispersion staining objectives. )

Dispersion staining can sometimes provide a fast and inexpensive laboratory technique to identify materials when the only alternative techniques are slow and expensive and not amenable to testing massive numbers of samples.

All comments to the author Robert Pavlis are welcomed.

  Microscopy UK Front Page
Micscape Magazine
Article Library